Method to solve Non-Linear Eqations

Bisection Method:-

#include<stdio.h>

#include<math.h>

float fun (float x)

{

    return (x*x*x - 4*x - 9);

}

void bisection (float *x, float a, float b, int *itr)

/* this function performs and prints the result of one iteration */

{

    *x=(a+b)/2;

    ++(*itr);

    printf("Iteration no. %3d X = %7.5f\n", *itr, *x);

}

void main ()

{

    int itr = 0, maxmitr;

    float x, a, b, allerr, x1;

    printf("\nEnter the values of a, b, allowed error and maximum iterations:\n");

    scanf("%f %f %f %d", &a, &b, &allerr, &maxmitr);

    bisection (&x, a, b, &itr);

    do

    {

        if (fun(a)*fun(x) < 0)

            b=x;

        else

            a=x;

        bisection (&x1, a, b, &itr);

        if (fabs(x1-x) < allerr)

        {

            printf("After %d iterations, root = %6.4f\n", itr, x1);

            return 0;

        }

        x=x1;

    }

    while (itr < maxmitr);

    printf("The solution does not converge or iterations are not sufficient");

    return 1;

}

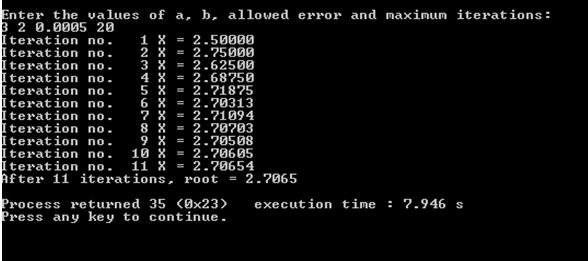
Output:-

Fixed Point Iteration Method:-

#include<stdio.h>

#include<math.h>

float raj(float);

main()

{

    float a[100],b[100],c=100.0;

    int i=1,j=0;

    b[0]=(cos(0)-3*0+1);

    printf("\nEnter initial guess:\n");

    scanf("%f",&a[0]);

    printf("\n\n The values of iterations are:\n\n ");

    while(c>0.00001)

    {

        a[j+1]=raj(a[j]);

        c=a[j+1]-a[j];

        c=fabs(c);

        printf("%d\t%f\n",j,a[j]);

        j++;

    }

    printf("\n The root of the given function is %f",a[j]);

}

float raj(float x)

{

    float y;

    y=(cos(x)+2)/3;

    return y;

}

Output:-

Regula Falsi Method:-

#include<stdio.h>

#include<math.h>

float f(float x)

{

    return cos(x) - x*exp(x);

}

void regula (float *x, float x0, float x1, float fx0, float fx1, int *itr)

{

    *x = x0 - ((x1 - x0) / (fx1 - fx0))*fx0;

    ++(*itr);

    printf("Iteration no. %3d X = %7.5f \n", *itr, *x);

}

void main ()

{

    int itr = 0, maxmitr;

    float x0,x1,x2,x3,allerr;

    printf("\nEnter the values of x0, x1, allowed error and maximum iterations:\n");

    scanf("%f %f %f %d", &x0, &x1, &allerr, &maxmitr);

    regula (&x2, x0, x1, f(x0), f(x1), &itr);

    do

    {

        if (f(x0)*f(x2) < 0)

            x1=x2;

        else

            x0=x2;

        regula (&x3, x0, x1, f(x0), f(x1), &itr);

        if (fabs(x3-x2) < allerr)

        {

            printf("After %d iterations, root = %6.4f\n", itr, x3);

            return 0;

        }

        x2=x3;

    }

    while (itr<maxmitr);

    printf("Solution does not converge or iterations not sufficient:\n");

    return 1;

}

Output:-

 FALSE POSITION METHOD:-

#include<stdio.h>

#include<conio.h>

#include<math.h>

#define ESP 0.0001

#define F(x) 3*(x) - 1 - cos(x)

void main()

{

  float x0,x1,x2,f1,f2,f0;

  int count=0;

  clrscr();

  do

  {

  printf("\nEnter the value of x0: ");

  scanf("%f",&x0);

  }while(F(x0) > 0);

  do

  {

  printf("\nEnter the value of x1: ");

  scanf("%f",&x1);

  }while(F(x1) < 0);

  printf("\n__________________________________________________________\n");

  printf("\n    x0\t       x1\t x2\t   f0\t   f1\t   f2");

  printf("\n__________________________________________________________\n");

  do

  {

  f0=F(x0);

  f1=F(x1);

  x2=x0-((f0*(x1-x0))/(f1-f0));

  f2=F(x2);

  printf("\n%f %f %f %f %f %f",x0,x1,x2,f0,f1,f2);

  if(f0*f2<0)

   {

    x1=x2;

   }

   else

   {

    x0 = x2;

   }

  }while(fabs(f2)>ESP);

printf("\n__________________________________________________________\n");

printf("\n\nApp.root = %f",x2);

getch();

}

 OUT PUT
---------
Enter the value of x0: -1

Enter the value of x1: 1

__________________________________________________________

    x0         x1        x2        f0      f1      f2
__________________________________________________________
-1.000000 1.000000 0.513434 -4.540302 1.459698 -0.330761
0.513434  1.000000 0.603320 -0.330761 1.459698 -0.013497
0.603320  1.000000 0.606954 -0.013497 1.459698 -0.000527
0.606954  1.000000 0.607096 -0.000527 1.459698 -0.000021
__________________________________________________________
App.root = 0.607096

Secant Method:-

#include<stdio.h>

float f(float x)

{

    return(x*x*x-4); // f(x)= x^3-4

}

float main()

{

    float a,b,c,d,e;

    int count=1,n;

    printf("\n\nEnter the values of a and b:\n"); //(a,b) must contain the solution.

    scanf("%f%f",&a,&b);

    printf("Enter the values of allowed error and maximun number of iterations:\n");

    scanf("%f %d",&e,&n);

    do

    {

        if(f(a)==f(b))

        {

            printf("\nSolution cannot be found as the values of a and b are same.\n");

        return;

        }

        c=(a*f(b)-b*f(a))/(f(b)-f(a));

        a=b;

        b=c;

        printf("Iteration No-%d    x=%f\n",count,c);

        count++;

        if(count==n)

        {

        break;

        }

    } while(fabs(f(c))>e);

    printf("\n The required solution is %f\n",c);

}

Output:-